Leistungsberechnung von Stirlingmotoren

Das ist Stirling-Alltag: Teile fertigen, montieren, abdichten, Leistungsmessungen machen, wieder zerlegen und neue Variante einbauen. Jedesmal in der Hoffnung auf ein paar Watt mehr. Jedesmal in der Gewißheit, weitere Erfahrungen gesammelt zu haben.

Aber – so will man meinen – eigentlich müsste sich ein Stirlingmotor doch auch berechnen lassen. Schließlich ist er eine thermodynamische Maschine. Und schon werden mit viel Mathematik die Gasgesetze bemüht und Onkel Computer darf im High-Tech-Zeitalter natürlich auch nicht fehlen. Ja, es gibt sogar seit einigen Jahren eine deutsche Software auf dem Markt (siehe unten). Einfach die Parameter eingeben, auf die Return-Taste drücken – und schon ist das Ergebnis da, ja, wenn man will sogar eine ganze Optimumkurve, einfach fantastisch. Dabei liegen die Abweichungen der modernen Programme zur Realität nur noch im Bereich von 5% - wirklich ein Fortschritt.

Nur, wer hat das Geld für das Programm und die Software? Geht es nicht auch einfacher?

Schon in den 70-er Jahren gab es eine einfache Formel zur Leistungsberechnung. Sie enthielt nur drei Parameter und ist daher leider nicht sehr genau. Hier ist sie in europäische Maßeinheiten übertragen:

P = 0,25 x p x V x n    darin:          P (Power)                  Leistung in W (Watt)

                                                           p (pressure)              Auflade-Druck in bar absolut

                                                           V (Volumen)            Hubvolumen Arbeitskolben in Liter

                                                           n                                 Drehzahl in U/min

Vater dieser empirischen Formel ist William Beale, Technischer Direktor der Firma Sunpower in den USA. 

Beale hatte seine Formel für Stirlingmotoren aufgestellt, die mit unter 30°C kaltem Wasser gekühlt und mit über 600°C heißen Erhitzern geheizt wurden. Das Temperaturverhältnis (TV) betrug also 873K / 303K = 2,88 bzw. etwas höher, so dass wir mit einem TV von 3 im Folgenden ausgehen.

Möchte man eine Kraft-Wärme-Kopplung realisieren oder sogar mit niedrigeren Temperaturen am Erhitzer arbeiten, so muss man die obere Formel von Beale weiter verändern:

P = 0,125 x p x V x n x (TV – 1)                            TV = Temperaturverhältnis in Kelvin

Die Beale-Zahl beträgt bei Einbeziehung des Temperaturverhältnisses den Wert von 0,125. Dies gilt für Motoren mit einem Phasenwinkel von 90°  und einer Drehzahl von über 2000 U/min. Solche Drehzahlen können nur Helium-Motoren unter Volllast erreichen. Wir brauchen also weitere Korrekturfaktoren, um die Leistung eines Stirlingmotors berechnen zu können. Diese Korrekturfaktoren sind an die Formel anzuhängen.

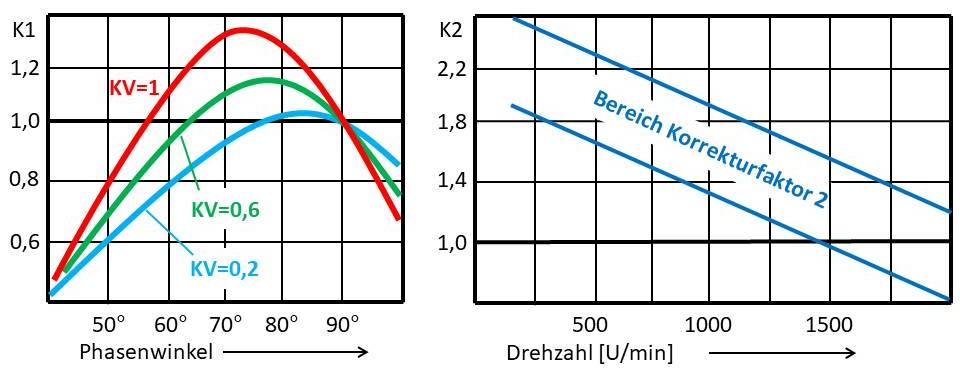
P = 0,125 x p x V x n x (TV - 1) x K1 x K2

Stirlingmotoren mit diskontinuierlichem Verdrängerhub, die den theoretischen Stirling-Zyklus noch besser nachahmen, besitzen generell einen höhere Beale-Zahl, Ridermotoren generell eine tiefere.

Schließlich soll gesagt werden, dass es  fünf Grenzen für die Anwendbarkeit oberstehender Formel gibt:

1.    Der Stirlingmotor muss ein echter Stirlingmotor sein, also kein Alpha-Typ.

2.  Die Dichtigkeit am Arbeitskolben muss einigermaßen gewährleistet sein, notfalls mit Kolbenringen

3.    Öl zur Schmierung und Dichtung des Kolbens und der Kolbenstange sollte wenn überhaupt aus extrem leichtläufigem Öl oder noch besser einem Gemisch aus Öl und Petrolium bestehen

4.    Die Regeneration muss nahezu vollständig sein (siehe Seite „Der Regenerator“) und

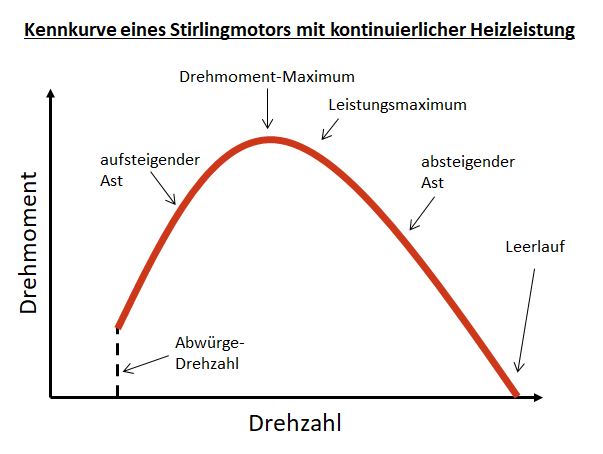
5.    Die Formel gilt nur für den aufsteigenden Drehzahl-Ast und das Leistungsmaximum, nicht für den hohen Drehzahl-Bereich eines Stirlingmotos Richtung Leerlauf.

Sicher ist diese empirische Formel noch nicht der Weisheit letzter Schluß. Aber bis in eine Leistungsklasse von einigen Kilowatt hinein sollte sie das zu Beginn beschriebene endlose Ausprobieren bei luftgeladenen Motoren ersetzen können.

Wer jetzt die Formel nach V umstellt, kommt zum Durchmesser und zum Hub des Arbeitskolbens (eine geringe Kurzhubigkeit ist angebracht: Hub gleich 0,8 des Durchmessers). Aber wie verhält es sich mit dem Hubvolumen des Verdrängerkolbens? Die Berechnung dieses Hubvolumens hängt vom Temperaturverhältnis ab und ist auf dieser Internetseite im Beitrag „Berechnung Biomassemotor“ genauer beschrieben.

Software zur Berechnung von  Stirling- und Ridermotoren:

Prosa 3.0 für 2200.Euro + MwSt, sowie Beratung und Berechnungsdienstleistung bei Prof. Bernd Thomas, Uni-Reutlingen

Mail: Bernd.Thomas@reutlingen-university.de

Homepage: http://userserv.hochschule-reutlingen.de/~thomas/

zurück zum Inhaltsverzeichnis (home).